以一个有监督的二分类模型,模型对每个样本的预测为一个概率值,我们需选取一个阈值(cutoff)来区分好坏用户
假定我们已经定好了一个阈值,超过此阈值定义为(目标用户)1,低于此阈值定义为非目标用户(0),就可以计算出混淆矩阵(confusion matrix)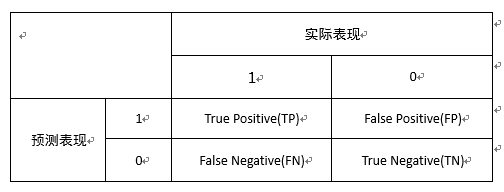
由上图我们可以得出TP.TN.FP.FN四个值。
- precision:TP/(TP+FP)
- recall:TP/(TP+FN)
- F1:precision和recall的调和均值F1=2PR/(P+R) 相当于综合指标
- Fα:F1的变体,Fα = (α^2+1)PR/(α^2P+R) 利用α给P、R赋不同权重
ROC曲线(receiver operating characteristing curve):是由多个混淆矩阵的结果组合,若在上述模型中没有定义好阈值,而是将模型预测结果从高到低排序,将每个概率值依次作为阈值,那么就要多个混淆矩阵。
对于每个混淆矩阵,计算2个指标:
- TPR(True positive rate): TP/(TP+FN),即为recall
- FPR(False positive rate): FP/(FP+TN),非目标中,预测为目标的占比
- 即TPR越高越好,FPR越低越好
- 我们以FPR为X轴,TPR为y轴画图,得到了ROC曲线
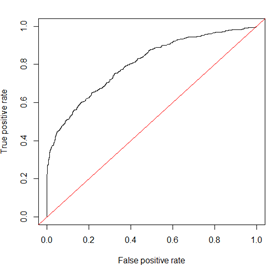
在画ROC曲线的过程中,若有一个阈值,高于此阈值的均为目标,低于这个阈值的均非目标,则该模型完美。ROC曲线经过(0,1)
AUC(Area Under Curve)的值为ROC曲线下面的面积,若上述模型十分准确,AUC为1。一般模型为0.5~1之间,AUC越高,模型区分能力越好。
Gini系数: 指ROC曲线与中线围成的面积和中线之上的面积与中线之下的面积(0.5)的比例,换算公式为Gini = 2*AUC-1
KS(Kolmogorov-Smirnov):KS=max(TPR-FRR),可以反映模型的最优区分效果,此时所取的阈值一般为最优阈值